Warning: package 'gt' was built under R version 4.3.314 Support Vector Machines
Support Vector Machines (SVM) sind eine Methode die sich besonders für Klassifikation von Beobachtungen bei komplexen, nicht-linearen Zusammenhängen in hoch-dimensionalen Datensätzen eignet. Anders als baum-basierte Methoden, die auf der Zerlegung des Regressorraums anhand binärer Entscheidungsregeln basieren (vgl. Kapitel 15), verwenden SVMs einen geometrischen Ansatz, der auf der Maximierung von Abständen beruht.
Das Ziel eines SVM-Modells ist es, eine Hyperebene (separating hyperplane) zu finden, die zwei (oder mehr) Klassen optimal voneinander trennt, indem der Abstand (margin) zwischen einer bestimmten Anzahl nächstgelegener Datenpunkten der verschiedenen Klassen maximiert wird. Diese Datenpunkte, die der Trennfläche am nächsten liegen, definieren die Klassifikationsregel des Modells und werden als Support-Vektoren (support vectors) bezeichnet. Bei einer hochgradig nicht-linearen Entscheidungsgrenzen können die ursprünglichen Beobachtungen mit einer Kernel-Funktion in einen höherdimensionalen Raum abgebildet werden in dem die Klassen linear trennbar sind.
Im Gegensatz zu Baum-basierten Modellen sind SVMs oft weniger intuitiv interpretierbar, da aus der angepassten Entscheidungsgrenze nicht unmittelbar die Relevanz der Regressoren abgeleitet werden kann.
In diesem Kapitel beschreiben wir die theoretischen Grundlagen von SVMs für Klassifikation von Beobachtungen hinsichtlich einer binären Outcome-Variable. Für technische Details und Beispiele empfehlen wir eine Aufarbeitung mit Kapitel 9 in James u. a. (2017).1 erläutern die Anwendung in R mit parsnip.
1 Hastie, Tibshirani, und Friedman (2013) geben eine ausführlichere, jedoch formal anspruchsvollere Erläuterung der hier behandelten Methoden.
14.1 Trennende Hyper-Ebenen
Wir betrachten zunächst ein Klassifikationsproblem mit zwei Prädiktoren \(X_1\), \(X_2\) für die binäre Outcome-Variable \(Y\). Die nächste Abbildung stellt diese Beobachtungen im Prädiktorraum graphisch dar. Mit geom_function() fügen wir dem Plot drei mögliche Trenneben hinzu, welche die Klassen perfekt separieren.
library(ggplot2)
library(cowplot)
# Visualisiere den Datensatz mit ggplot2
ggplot(
data = lsvm_data,
mapping = aes(x = x1, y = x2, color = klasse)
) +
geom_point(size = 3) +
labs(x = "X1", y = "X2") +
# Mögliche Trennebenen
geom_function(fun = \(x) -1.5 * x, col = "black") +
geom_function(fun = \(x) -2.5 * x, col = "black") +
geom_function(fun = \(x) -.4 * x, col = "black") +
lims(y = c(-5, 6)) +
theme_cowplot() +
theme(legend.position = "top")
14.1.1 Trennebenen
SVM für Klassifikation basiert auf der Idee, eine Trennhyperebene \[\begin{align} \boldsymbol{w}'\boldsymbol{X} + b = 0 \label{eq:sepplane} \end{align}\] im Prädiktorraum zu finden, welche die Datenpunkten hinsichtlich ihrer Klasse möglichst gut trennt.
Definiere die abhängige Variable als \[\begin{align*} y = \begin{cases} -1, & \textup{wenn Beob. $i$ Klasse A hat,}\\ 1, & \textup{wenn Beob. $i$ Klasse B hat} \end{cases} \end{align*}\]
Wähle \(\boldsymbol{w}\) und \(b\) so, dass die Ungleichung
\[\begin{align} y_i(\boldsymbol{w}'\boldsymbol{X}_i + b) \geq 0 \label{eq:sepcond} \end{align}\]
erfüllt ist, d.h.
\[\begin{align*} \boldsymbol{w}'\boldsymbol{X}_i + b \geq 0 & \quad \textup{für} \quad y_i = 1,\\ \boldsymbol{w}'\boldsymbol{X}_i + b \leq 0 & \quad \textup{für} \quad y_i = -1. \end{align*}\]
In unserem Beispiel mit zwei Regressoren \(X_1\), \(X_2\) ist \(\boldsymbol{w} = (w_1,\,w_2)'\) und \(\boldsymbol{X}=(X_1,\,X_2)'\). Der Prädiktorrraum ist also zwei-dimensional. Jede Hyperebene in diesem Raum ist ein-dimensional, kann also formal durch eine Geraden-Gleichung der Form \[\begin{align} x_2 = \alpha_1\cdot x_1 + \alpha_0 \label{eq:gg} \end{align}\] dargestellt werden: Durch Umformen von \(\eqref{eq:sepplane}\) erhalten wir \[\begin{align} &\, w_1 \cdot x_1 + w_2 \cdot x_2 + b = 0 \notag \\ \\ \Leftrightarrow &\, x_2 = -\left(\frac{w_1}{w_2}\right) \cdot x_1 - \frac{b}{w_2} \label{eq:ggt} \end{align}\]
In Abbildung XYZ erkennen wir, dass die Beobachtungen durch eine Gerade mit negativer Steigung perfekt separiert werden können.
Wenn die Daten perfekt separierbar sind (und die Regressoren kontinuierlich sind) gibt es unendlich viele Ebenen, die Bedingung \(\eqref{eq:sepcond}\) erfüllen. Welche Hyperebene (also welche Parameter \(\boldsymbol{w},\,b\)) gewählt werden sollen, muss durch weitere Bedingungen festgelegt werden.
14.1.2 Maximal Margin Classifier
Ein Maximal Margin Classifier (MMC) wählt die trennende Ebene wie folgt: Bestimme \(\{\boldsymbol{w},b\}\) und \(M\) unter der Bedingung \(\sum_{j=1}^k w_j^2 = 1\) so, dass für sämtliche Beobachtungen gilt, dass
\[\begin{align*} Y_i(\boldsymbol{w}'\boldsymbol{X}_i + b) \geq M, \quad \forall i \in \{1, \dots, n\}, \end{align*}\]
wobei \(M\), der minimale Abstand aller Beobachtungen zur trennenden Ebene – die Margin – maximiert wird.
Beobachtungen, die exakt die Distanz \(M\) zur Trennebene haben, sind die Support-Vektoren (SV). Beachte: Ausschließlich die SV definieren die angepasste Entscheidungsgrenze des MMC.
Wir trainieren nun einen MMC für klasse in lsvm_data mit e1071::svm(). Mit kernel = "linear" legen wir fest, dass eine lineare Entscheidungsgrenze im zwei-dimensionalen Raum von \((X_1,X_2)\) gefunden werden soll. Die Parameter cost = 1e8 und scale = F erzwingen wir eine “harte” Margin (mehr dazu im Abschnitt zu SVMs unten) sowie keine Skalierung der Daten. Mit coef() lesen wir die trainierten Koeffizienten aus.
library(e1071)
# Trainiere das Modell
model_mm <- svm(
klasse ~ x1 + x2,
data = lsvm_data,
kernel = "linear",
cost = 1e8,
scale = F
)
# Trainierte Koeffizienten des MMC auslesen
(
coefs <- coef(model_mm) %>%
set_names(
c("b", "w1", "w2")
)
) b w1 w2
0.06210578 -0.52107776 -0.69398704 Zur Vereinfachung der graphischen Darstellung normieren wir den Vektor der Koeffizienten c("w1", "w2").
# Koeffizienten normieren
nrm <- sqrt(coefs["w1"]^2 + coefs["w2"]^2) # Euklidische Norm
coefs <- coefs / nrmMit den angepassten Koeffizienten in coefs können wir anhand der Umformung \(\eqref{eq:ggt}\) die mit MMC ermittelte trennende Gerade berechnen. Wir definieren \(\alpha_0\) und \(\alpha_1\) wie in \(\eqref{eq:gg}\).
# Koeffizienten der trennenden Geraden berechnen
# alpha0
(
alpha0 <- unname(-coefs["b"] / coefs["w2"])
)[1] 0.08949127# alpha1
(
alpha1 <- unname(-coefs["w1"] / coefs["w2"])
)[1] -0.7508465Der Eintrag SV des im Objekt model_mm gespeicherten Outputs von svm() enthält die Support-Vektoren des MMC.
# A tibble: 3 × 2
x1 x2
<dbl> <dbl>
1 0.416 -1.66
2 3.01 -0.732
3 0.0518 1.49 Mit geom_function() zeichnen wir nun die ermittelte Trennlinie in den Punkteplot der Regressoren ein. Wir ergänzen die Grafik um die Marginallinien und Hervorhebungen der in sv gespeicherten Support-Vektoren.
# Beobachtungen in MMC-Trennlinien einzeichnen
ggplot(
data = lsvm_data,
mapping = aes(x = x1, y = x2, color = klasse)
) +
labs(x = "X1", y = "X2") +
# Trennlinie
geom_function(
fun = \(x) alpha0 + alpha1 * x, col = "black"
) +
# Marginallinien
geom_function(fun = \(x) -(coefs[1] + 1/nrm)/coefs[3] + alpha1 * x,
col = "black", linetype = "dashed") +
geom_function(fun = \(x) -(coefs[1] - 1/nrm)/coefs[3] + alpha1 * x,
col = "black", linetype = "dashed") +
# Support-Vektoren
geom_point(
data = sv,
mapping = aes(x = x1, y = x2),
size = 5,
shape = 1,
inherit.aes = F
) +
# Beobachtungen
geom_point(size = 2) +
lims(y = c(-3, 6), x = c(-3.8, 3.8)) +
theme_cowplot() +
theme(legend.position = "top")Warning: Removed 22 rows containing missing values or values outside the scale range
(`geom_function()`).Warning: Removed 12 rows containing missing values or values outside the scale range
(`geom_point()`).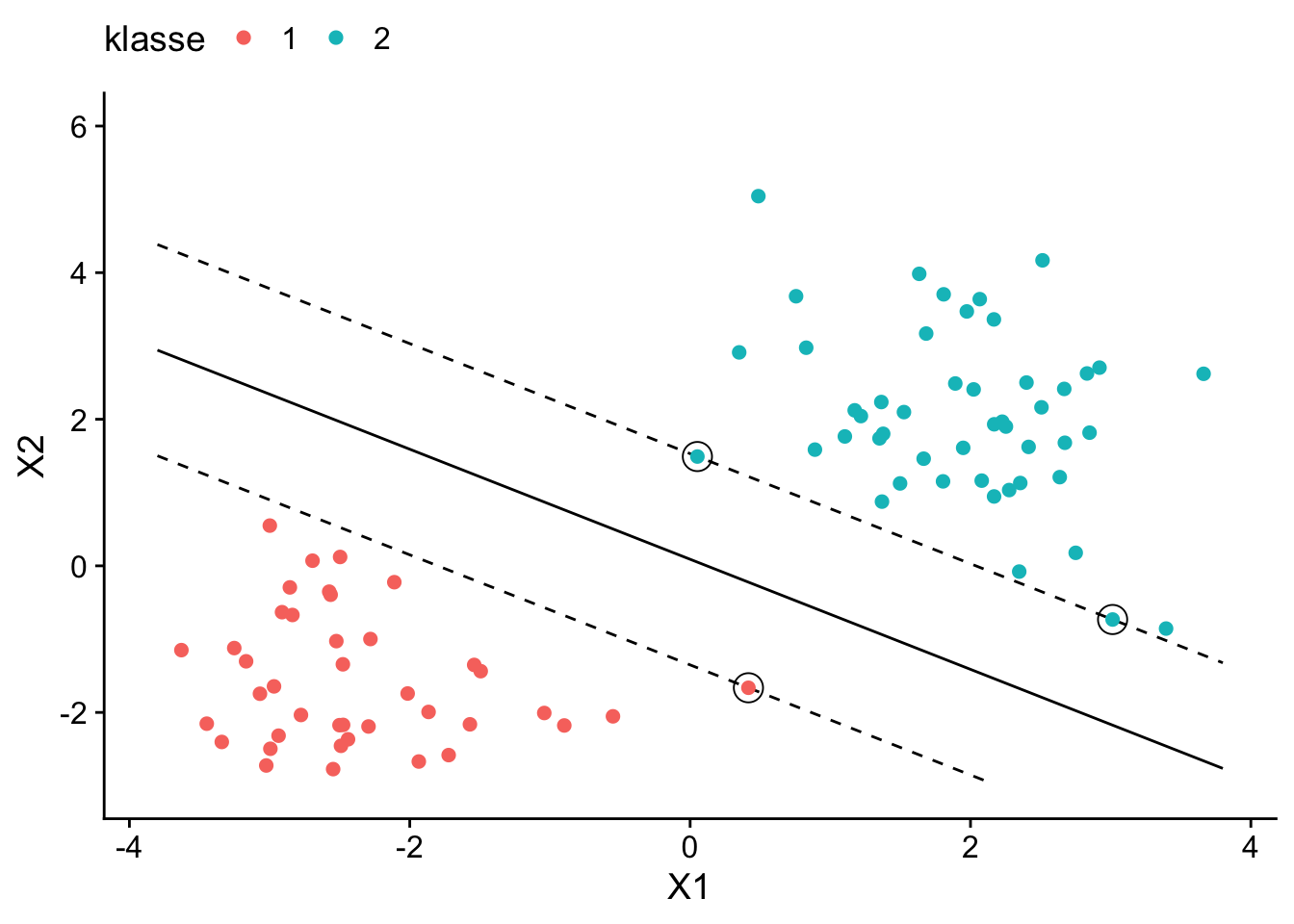
Die Grafik zeigt, dass der MMC in model_mm tatsächlich eine perfekte Klassifzierung der Datenpunkte erreicht: Die gewählte Trennlinie (schwarze Linie) maximiert die jeweils durch die Marginallinien (getrichelte Linien) definierte Margin. Der MMC wird lediglich durch die 3 schwarz umrandeten Beobachtungen (die Support-Vektoren) definiert.
Wir können die Genauigkeit der Klassifikation von model_mm für die Trainingsdaten mit yardstick::accuracy auswerten.
Attaching package: 'yardstick'The following object is masked from 'package:readr':
spec# Genauigkeit der Klassifizierung für Trainingsdaten
model_mm %>%
predict() %>%
bind_cols(
estimate = .,
truth = lsvm_data$klasse
) %>%
accuracy(truth, estimate)# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy binary 1Ein Nachteil des MMC ist, dass das training der separierenden Grenze empfindlich gegenüber Ausreißern und hoher Varianz in den Daten ist: Da der MMC die Trennlinie so positioniert, dass der Abstand (die “Margin”) zu den nächstgelegenen Trainingsdatenpunkten maximal wird, können selbst wenige ungewöhnliche Beobachtungen die Lage der Grenze stark beeinflussen, was die Robustheit des Classifier beeinträchtigt und zu einer schlechteren Generalisierung auf neue Daten führen kann.
Abbildung 14.2 illustriert die Sensibilität des MMC durch Hinzufügen nur einer zusätzlichen ungewöhnlichen Beobachtung der Klasse 1 mit \(X_1 = -.5\) und \(X_2 = 3\)2: Das Optimierungskalkül des MMC führt zu einer deutlich verschobenen Trennlinie im Vergleich zu ABZ.
2 Der Code hierfür ist lsvm_data %>% add_row(tibble(x1 = -.5, x2 = 3, klasse = factor(1))).
Warning: Removed 78 rows containing missing values or values outside the scale range
(`geom_function()`).
Removed 78 rows containing missing values or values outside the scale range
(`geom_function()`).
Removed 78 rows containing missing values or values outside the scale range
(`geom_function()`).Warning: Removed 12 rows containing missing values or values outside the scale range
(`geom_point()`).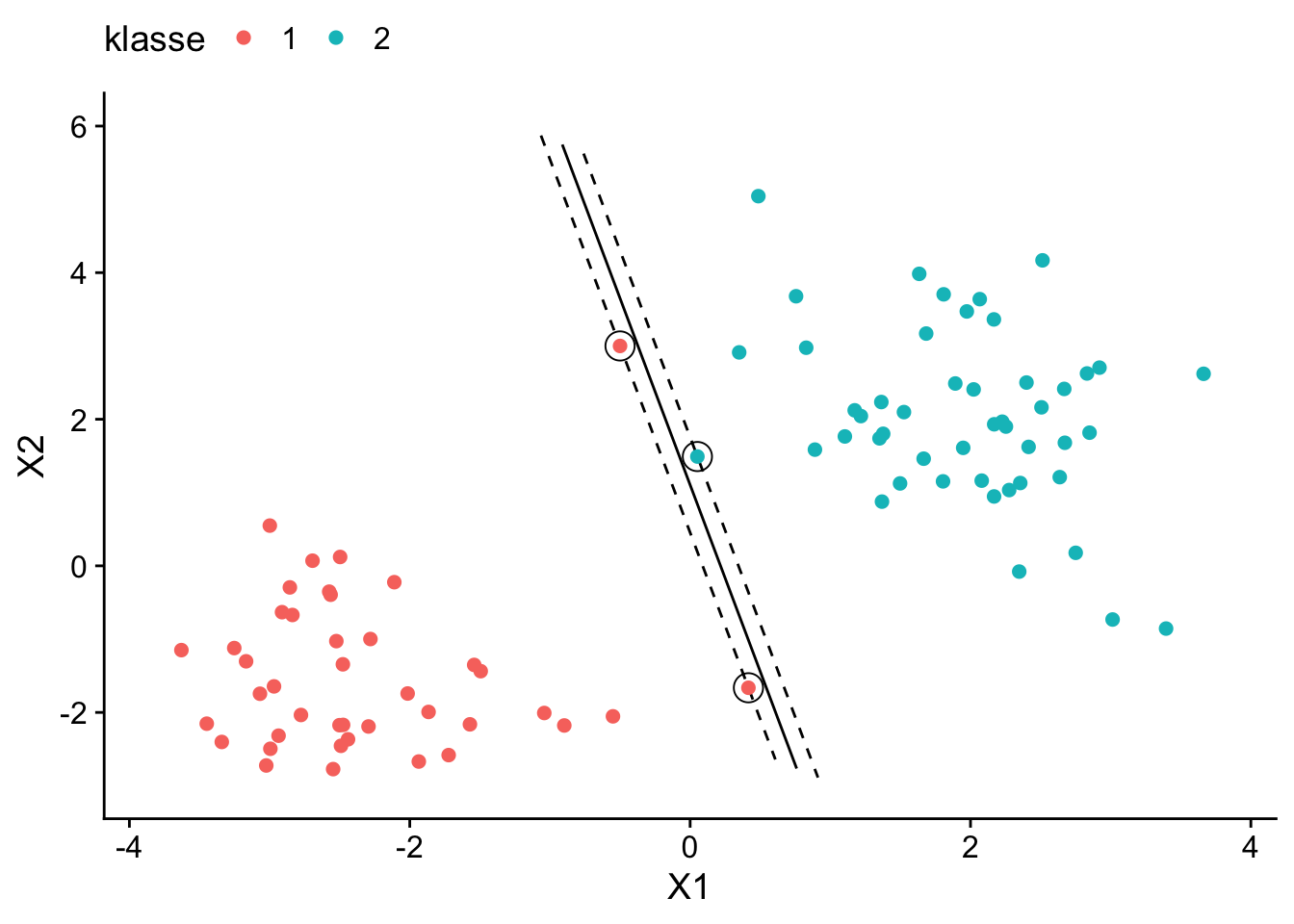
Eine Erweiterung des MMC, die dieses Problem adressiert ist der (Soft Margin) Support Vector Classifier (SVC). Der Ausreißer lässt bestimmte Fehlklassifizierungen zu, um eine bessere Balance zwischen Genauigkeit auf dem Trainingsdatensatz und Generalisierungsfähigkeit des Modells zu finden.
14.2 Support Vector Classifier
Ein MMC strebt eine strikte Trennung der Datenklassen durch eine Hyperebene mit einer “harten” Margin, deren Grenzen durch die Support-Vektoren definierten werden (hard margin). Ein SVC erlaubt eine “weiche” Margin (soft margin) die zu weniger Empfindlichkeit der ermittelten Enscheidungsgrenze gegenüber Rauschen und Ausreißern führt. Diese weiche Margin lässt zu, dass Beobachtungen innerhalb der Margin liegen und erlaubt auch Fehlklassifikationenen. Die Support-Vektoren des SVC sind sämtliche Beobachtungen, di im Bereich der Margin liegen.
Wie beim MMC ist es das Ziel des SVC, die Parameter \(\{\boldsymbol{w}, b\}\) so zu bestimmen, dass die Margin maximiert wird, jedoch dürfen einige Datenpunkte innerhalb der Margin oder sogar auf der falschen Seite der trennenden Hyperebene (Fehlerklassifizierung) liegen. Ein SVC kann so eine (nicht perfekt) trennende Hyperbene finden, wenn das Optimierungskalkül des MMC aufgrund der Überlappung der Klassen unlösbar ist.
Hierzu wird die Ebene unter Berücksichtigung einer weiteren Bedingung für die Optimierung ermittelt, die auf Slack-Variablen \(\epsilon_i \geq 0\) basiert,
\[\begin{align} \sum_{i=1}^{n} \epsilon_i \leq C. \label{eq:svcreg} \end{align}\]
Die \(\epsilon_i\) sind größer 0 für Beobachtungen, welche die Margin verletzen, wobei die Größe von \(\epsilon_i\) die Intensität der Verletzung misst. Für eine Beobachtung \(i\) innerhalb der Margin, aber auf der korrekten Seite der Trennebene ist \(0\leq\epsilon_i<1\). Liegt die Beobachtung auf der falschen Seite der Ebene, ist \(\epsilon_i>1\).
\(C\geq0\) ist ein Regularisierungsparameter, der die Balance zwischen der Maximierung der Margin und der Anzahl der tolerierten Fehlklassifikationen regelt.3 Ein hoher Wert von \(C\) ermöglicht mehr Verletzungen der Margin und mehr Fehlklassifikationen, was meist zu einer breiteren Margin führt. Ein kleinerer Wert von \(C\) hingegen erzielt eine kleinere Margin mit weniger Verletzungen und Fehlklassifikationen. \(C\) ist also ein Tuning-Parameter der einen Bias-Varianz-Tradeoff regelt: Für kleine \(C\) (kleine Margins) wird die trennende Ebene gut an die Trainingsdaten angepasst, hat also wenig Verzerrung aber tendentiell größere Varianz. Für große \(C\) (breite Margin) ist die Varianz beim Bestimmen der trennenden Ebene tendentiell kleiner, jedoch kann die Verzerrung groß sein. Diese Abwägung ist wichtig für die Güte der Klassifizierung neuer Beobachtung. In empirischen Anwendungen wird \(C\) mit Cross-Validation bestimmt.
3 Für \(C=0\) muss \(\sum_{i=1}^{n} \epsilon_i = 0\) sein. Der SVC entspricht dann dem MMC.
Nicht perfekt separierbare Klassen
# nicht exakt separierbare Daten einlesen
lsvm_nonsep_data <- readRDS(file = "datasets/lsvm_nonsep_data.RDS")ggplot(
data = lsvm_nonsep_data,
mapping = aes(x = x1, y = x2, color = klasse)
) +
labs(
x = "X1",
y = "X2",
title = "Nicht perfekt separierbare Klassen"
) +
# Beobachtungen
geom_point(size = 2) +
theme_cowplot() +
theme(legend.position = "top")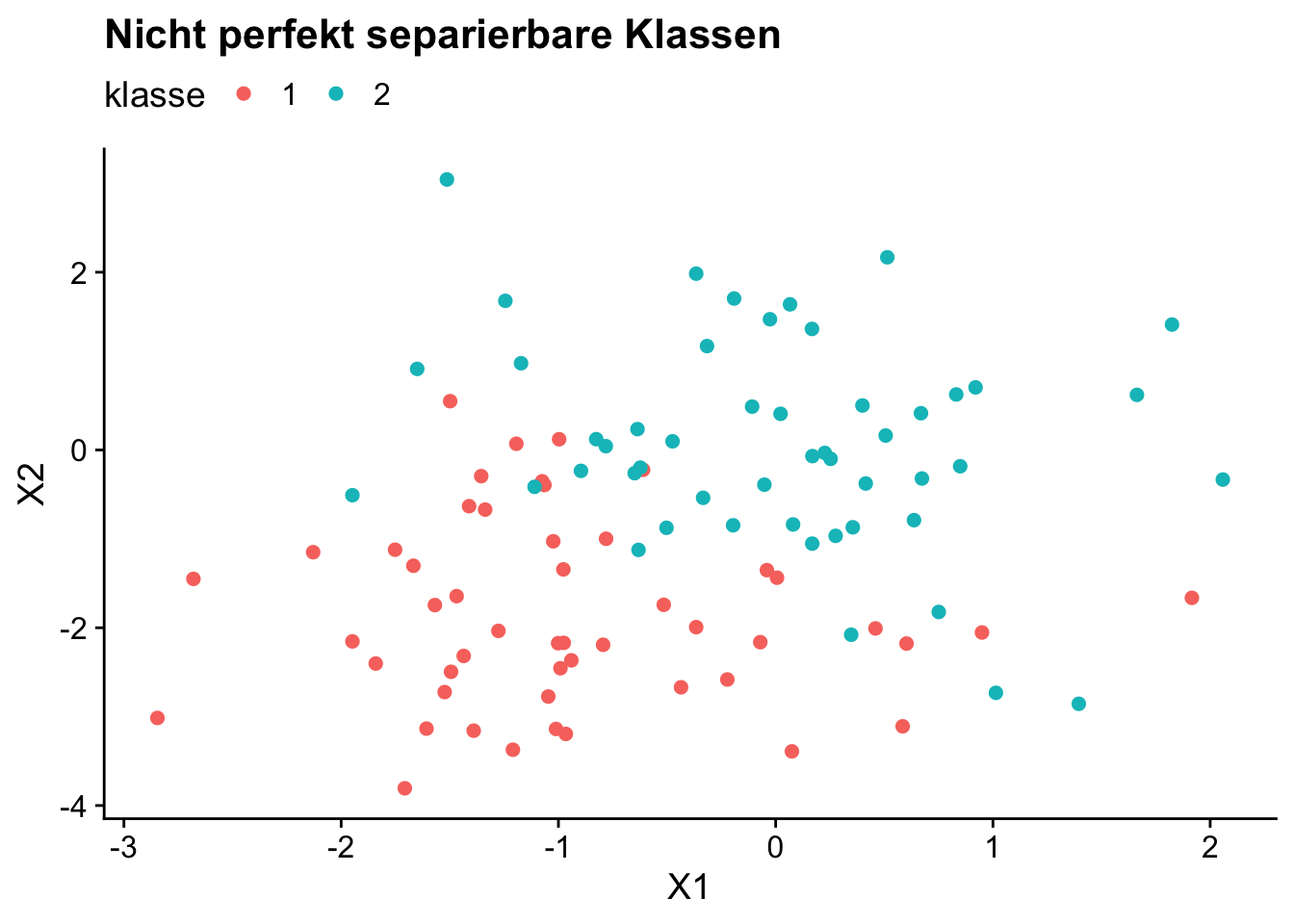
Ein MMC kann für den in Abbildung 14.3 gezeigten Datensatz lsvm_nonsep_data keine Lösung finden: Der Algorithmus iteriert bis zu einer maximalen Anzahl an Durchläufen.
Ein SVC hingegen kann angepasst werden: Mit cost = 1 räumen wir ein “Budget” für Verletzungen der Margin und Fehlklassifikationen ein.4
4 Der Parameter cost in svm() ist ein Lagrange-Multiplikator und verhält sich daher invers zu \(C\) in \(\eqref{eq:svcreg}\): Große Werte für cost führen zu viel Regularisierung (kleine Margin) und umgekehrt.
# Trainiere ein SVC-Modell
model_svc <- svm(
klasse ~ x1 + x2,
data = lsvm_nonsep_data,
kernel = "linear",
cost = 1,
scale = F
)
model_svc
Call:
svm(formula = klasse ~ x1 + x2, data = lsvm_nonsep_data, kernel = "linear",
cost = 1, scale = F)
Parameters:
SVM-Type: C-classification
SVM-Kernel: linear
cost: 1
Number of Support Vectors: 36# Trainierte Koeffizienten des SVC auslesen
(
coefs <- coef(model_svc) %>%
set_names(
c("b", "w1", "w2")
)
) b w1 w2
-1.998007 -1.525909 -1.336617 Analog zu model_mmc können wir die trennende Gerade gemeinsam mit den Margins sowie den SV graphisch darstellen.
ggplot(
data = lsvm_nonsep_data,
mapping = aes(x = x1, y = x2, color = klasse)
) +
labs(x = "X1", y = "X2") +
# Trennlinie
geom_function(
fun = \(x) alpha0 + alpha1 * x, col = "black"
) +
# Marginallinien
geom_function(fun = \(x) -(coefs[1] + 1/nrm)/coefs[3] + alpha1 * x,
col = "black", linetype = "dashed") +
geom_function(fun = \(x) -(coefs[1] - 1/nrm)/coefs[3] + alpha1 * x,
col = "black", linetype = "dashed") +
# Support-Vektoren
geom_point(
data = sv,
mapping = aes(x = x1, y = x2),
size = 5,
shape = 1,
inherit.aes = F
) +
# Beobachtungen
geom_point(size = 2) +
theme_cowplot() +
theme(legend.position = "top")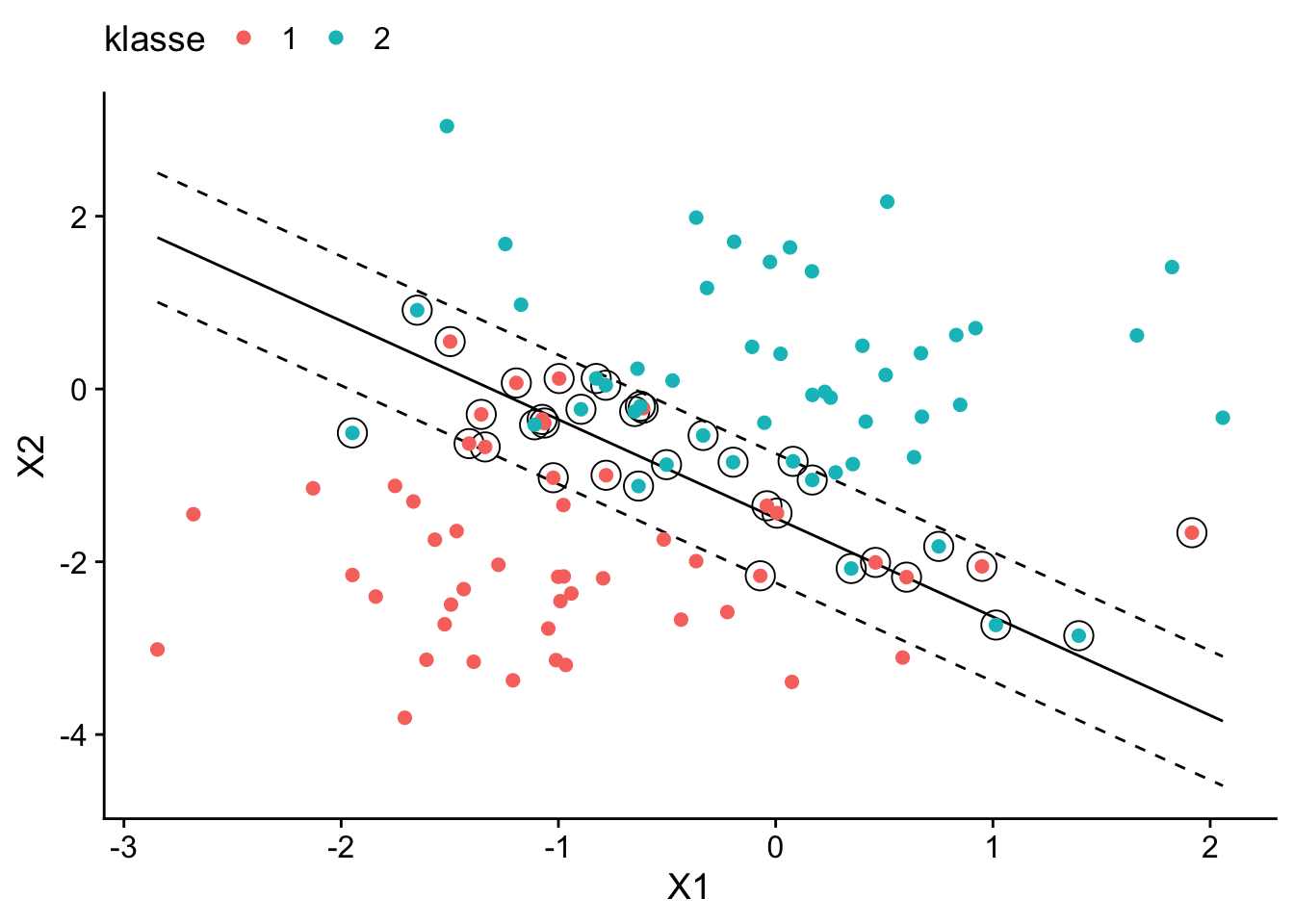
Aufgrund der Soft Margin des SVC werden hier Fehlklassifikationen in Kauf genommen. Beachte, dass sowohl Beobachtungen auf und innerhalb der Margin als auch fehlklassifizierte Beobachtungen die Support-Vektoren der trennenden Geraden sind in Abbildung 14.4 sind.
# Genauigkeit der Klassifizierung für Trainingsdaten
model_svc %>%
predict() %>%
bind_cols(
estimate = .,
truth = lsvm_nonsep_data$klasse
) %>%
accuracy(truth, estimate)# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 accuracy binary 0.85Nicht-lineare und unscharfe Entscheidungsgrenzen
In empirischen Anwendungen gibt es selten exakt lineare Entscheidungsgrenzen. Wir präsentieren nun ein Beispiel für eine nicht-lineare Entscheidungsgrenze, bei der SVC dennoch eine hilfreiche Approximation der Entscheidungsgrenze liefern kann und diskutieren anschließend Support Vector Machines als Generalisierung von SVC zur Anpassung nicht-linearer Grenzen.
Der Datensatz data_wavy enthält gleichverteilte Beobachtungen \((X_1, X_2)\) die gemäß der sinusoidalen Entscheidungsgrenze
\[\begin{align*} g(x_1) = x_1 + 3\cdot \sin(1.2 \cdot x_1), \end{align*}\]
in zwei Klassen eingeteilt sind: Beoabchtungen gehören zu Klasse 1, wenn \(x_2 + \varepsilon > g(x_1)\) und ansonsten zu Klasse 2. Der (normalverteilte) Fehlerterm \(\varepsilon\) führt zu einer unscharfen Trennung der Klassen, d.h. der Trainingsdatensatz ist selbst bei Abgleich mit der (nachfolgend als unbekannt angenommenen) Funktion \(g(x_1)\) nicht vollständig korrekt klassifizierbar. Wir suchen dennoch einen Classifier, der \(g(x_1)\) gut approximiert, also den deterministischen Teil der Entscheidungsregel möglichst gut lernt.
# data_wavy einlesen
data_wavy <- readRDS("datasets/data_wavy.RDS")Zunächst plotten wir die Beobachtungen in data_wavy gemeinsam mit der deterministischen Entscheidungsgrenze \(g(x_1)\).
# Visualisiere den Datensatz mit ggplot2
ggplot(
data = data_wavy,
mapping = aes(
x = x1,
y = x2,
color = klasse
)
) +
geom_point() +
labs(
x = "X1",
y = "X2"
) +
# deterministische Entscheidungsgrenze
geom_function(
fun = \(x) x + 3 * sin(x * 1.2),
lwd = 1.25
) +
coord_equal(expand = F) +
theme_cowplot() +
theme(legend.position = "top")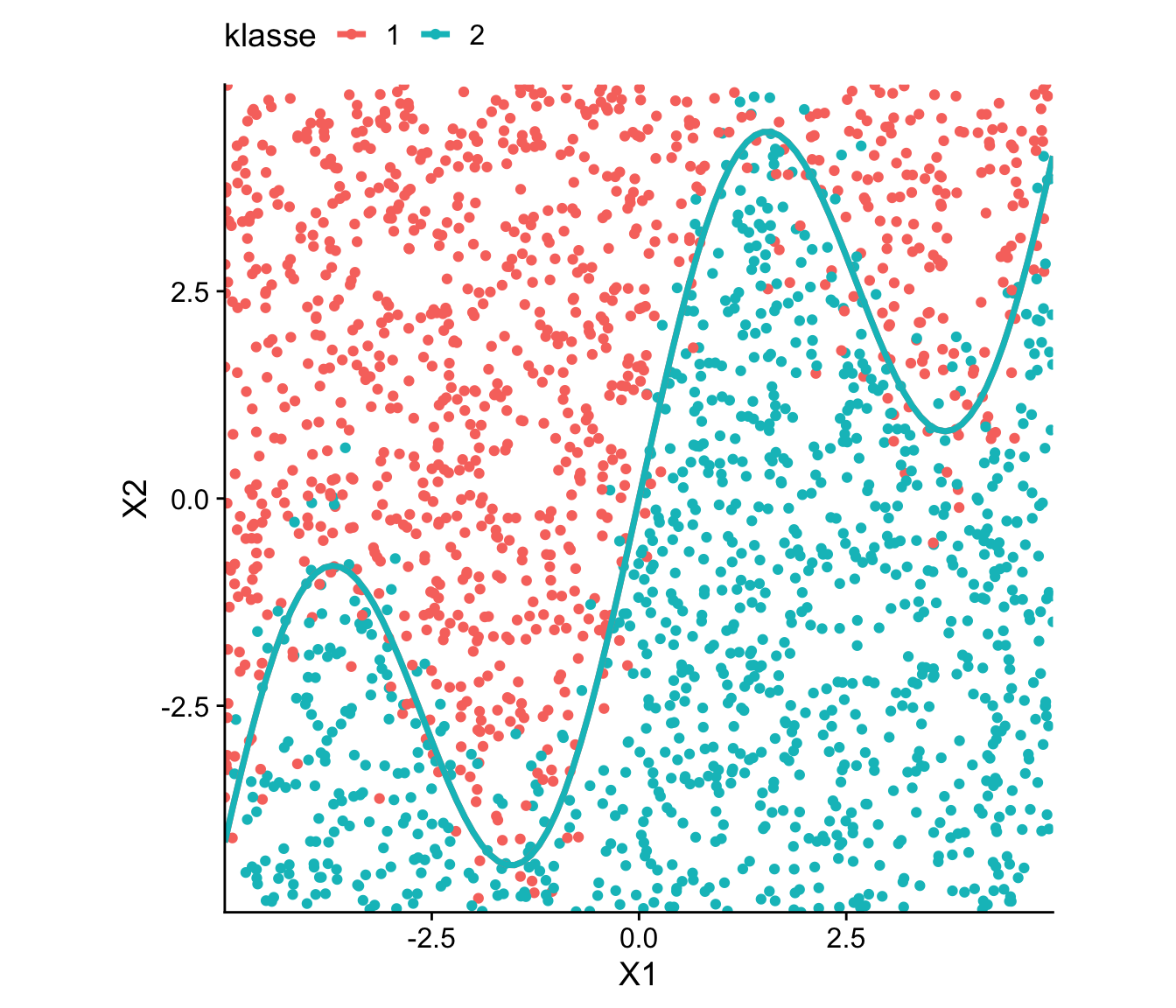
data_wavy: Beobachtungen mit nicht-linearer Entscheidungsgrenze
Ein SVC kann die nicht-lineare Entscheidungsgrenze nicht abbilden, erreicht jedoch aufgrund der groben Teilbarkeit des Regressorraums hinsichtlich der Klassen durch eine (von links unten nach rechts oben verlaufende) Grade eine akzeptable Fehlklassifikationsrate. Wir zeigen dies mit R.
# Trainiere SV Classifier mit Cost-Kriterium
svc_wavy <- svm(
klasse ~ .,
data = data_wavy,
kernel = "linear",
cost = 1,
scale = F
)
svc_wavy
Call:
svm(formula = klasse ~ ., data = data_wavy, kernel = "linear", cost = 1,
scale = F)
Parameters:
SVM-Type: C-classification
SVM-Kernel: linear
cost: 1
Number of Support Vectors: 849# Daten + Entscheidungsgrenze mit ggplot
ggplot() +
geom_point(
data = grid,
mapping = aes(x = x1, y = x2, color = klasse), alpha = 0.1) +
geom_point(
data = data_wavy,
mapping = aes(x = x1, y = x2, color = klasse)) +
geom_function(
fun = \(x) x + 3 * sin(x * 1.2),
col = "#00BFC4",
lwd = 1.25
) +
labs(x = "X1", y = "X2") +
coord_equal(expand = F) +
theme_cowplot() +
theme(legend.position = "top")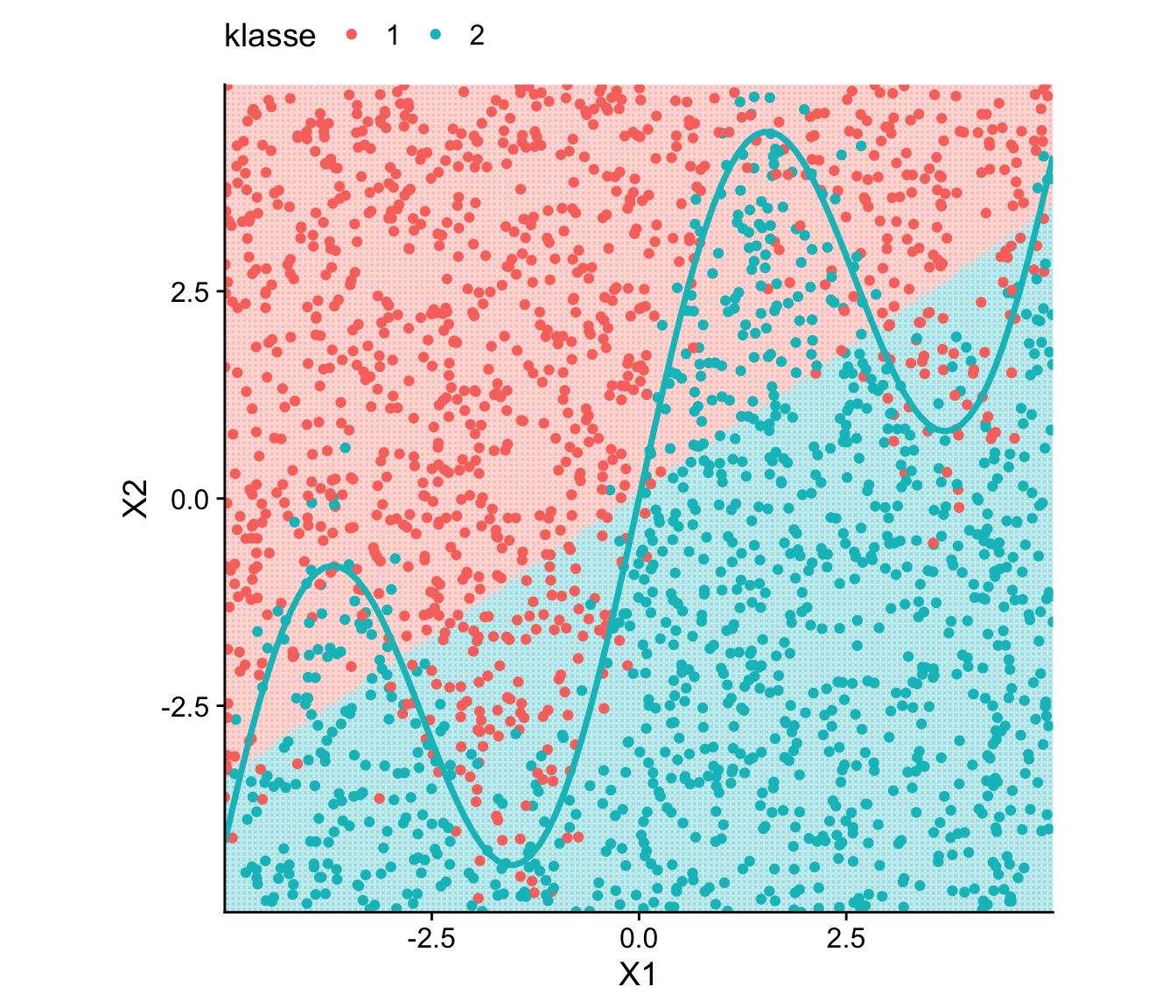
data_wavy: Mit SVC trainierte und deterministische Entscheidungsgrenze
[1] 0.1835Diese Fehlerrate kann durch Verfahren, die nicht-lineare Entscheidungsgrenzen lernen können, deutlich verringert werden. Der nächste Abschnitt erläutert eine entsprechende Erweiterung des SVC: Support Vector Machines.
14.3 Support Vector Machines
Sei \(S\) die Indexmenge der zu findenden Support-Vektoren für den SVC. Mann kann zeigen (vgl. Hastie, Tibshirani, und Friedman 2013), dass die zu lernende Entscheidungsregel des SVC die Form
\[\begin{align} f(x) = b + \alpha_i \sum_{i\in S} \langle\boldsymbol{x},\boldsymbol{x}_j\rangle \label{eq:svck} \end{align}\]
hat, wobei \(\langle\boldsymbol{x}_i,\boldsymbol{x}_j\rangle\) das innere Produkt der Vektoren \(\boldsymbol{x}_i\) und \(\boldsymbol{x}_j\) meint,
\[\begin{align*} \langle\boldsymbol{x}_i,\boldsymbol{x}_j\rangle := \sum_{l=1}^k x_{i,l} x_{j,l}. \end{align*}\]
Die Funktion \(\langle\boldsymbol{x}_i,\boldsymbol{x}_j\rangle\) ist ein Beispiel für eine Kernel-Funktion \(K(\boldsymbol{x}_i,\boldsymbol{x}_j)\), der lineare Kernel. Ein Kernel \(K\) berechnet die “Ähnlichkeit” zwischen zwei Datenpunkten. Mit \(K(\boldsymbol{x}_i,\boldsymbol{x}_j)=\langle\boldsymbol{x}_i,\boldsymbol{x}_j\rangle\) wird die lineare Übereinstimmung der Vektoren \(\boldsymbol{x}_i\) und \(\boldsymbol{x}_j\) im ursprünglichen Regressorraum gemessen und damit eine lineare Klassifikationsregel \(f(x)\) gesucht.5
5 Geometrisch wird die Ähnlichkeit durch den Winkel zwischen den Regressor-Vektoren gemessen: \(\langle\boldsymbol{x}_i \boldsymbol{x}_j\rangle = \|\boldsymbol{x}_i\| \|\boldsymbol{x}_j\| \cos(\theta)\), wobei \(\theta\) der Winkel zwischen \(\boldsymbol{x}_i\) und \(\boldsymbol{x}_j\) ist.
6 Der Kernel Trick ist hilfreich, weil die explizite Transformation der Daten rechenaufwendig oder sogar unlösbar sein kann. Kernel-Funktionen hingegen können schnell berechnet werden.
Eine Support Vector Machine (SVM) ersetzt das innere Produkt in \(\eqref{eq:svck}\) durch einen nicht-linearen Kernel \(K\). Dadurch können SVMs auch hochgradig nicht-lineare Entscheidungsgrenzen lernen: Um die nicht-lineare Beziehungen in den Daten zu modellieren, werden die Regressoren mit einem \(K\) implizit so transformiert, dass sie in einem (möglicherweise hoch-dimensionalen) Raum einfacher hinsichtlich ihrer Klasse getrennt werden können. Diese Transformation muss jedoch dank des Kernels nicht explizit berechnet werden — dies ist der Kernel Trick.6
Typische nicht-lineare Kernel-Funktionen sind
-
Radialer Kernel
\[\begin{align*} K(\boldsymbol{x}_i,\boldsymbol{x}_j) = \exp\bigg(-\gamma \sum_{l=1}^k (x_{lj} - x_{li})^2\bigg) \end{align*}\]
-
Polynomialer Kernel (Ordnung \(d\))
\[\begin{align*} K(\boldsymbol{x}_i,\boldsymbol{x}_j) = \bigg(c + \sum_{l=1}^k x_{lj} \cdot x_{li} \bigg)^d, \quad c\in\mathbb{R},\ d>1 \end{align*}\]
-
Sigmoidaler Kernel
\[\begin{align*} K(\boldsymbol{x}_i,\boldsymbol{x}_j) = \tanh\bigg(\gamma\sum_{l=1}^k x_{lj} \cdot x_{li} + c \bigg), \quad c\in\mathbb{R} \end{align*}\]
Zusätzlich zu dem Tuning-Parameter \(C\) müssen also für das Training einer Entscheidungsgrenze die Skalierungs- bzw. Positions-Parameter \(\gamma\) und \(c\) für den Kernel gewählt werden. Letzteres erfolgt in empirischen Anwendungen häufig mit Cross-Validation.
14.3.1 Der Kernel-Trick
Um den Kernel Trick zu veranschaulichen, betrachten wir ein binäres Klassifikationsproblem mit einer nicht-linearen Entscheidungsgrenze im Regressorraum für \((X_1,X_2)\in\mathbb{R}^2\), bei dem die Klassenzugehörigkeit der Beobachtungen konzentrisch angeordnet ist. Wir lesen hierzu den Datensatz data_concentric ein.
# konzentrische Daten einlesen
data_concentric <- readRDS(
file = "datasets/data_concentric.RDS"
)Für einen Verständnis der Verteilung der Klassenzugehörigkeit im Regressorraum visualisieren wir den Datensatz data_concentric mit ggplot().
library(ggplot2)
library(cowplot)
# `data_concentric` visualisieren
ggplot(
data = data_concentric,
mapping = aes(x = X1, y = X2, color = klasse)
) +
geom_point() +
# Seitenverhältnis auf 1 setzten
coord_equal() +
theme_cowplot() +
theme(legend.position = "top")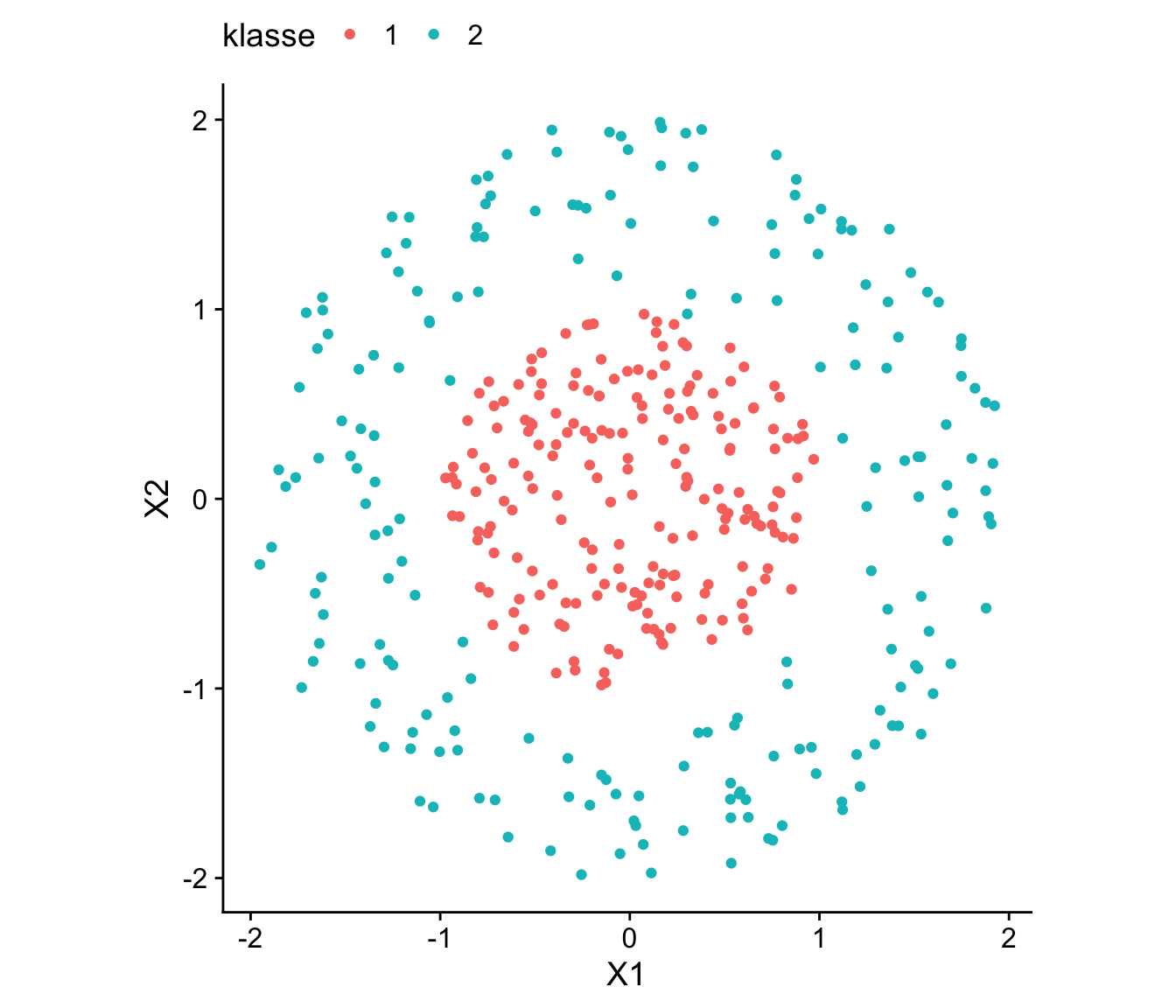
Die Klassen der in Abbildung 14.7 gezeigten Beobachtungen sind aufgrund der konzentrischen Verteilung nicht linear separierbar – die Entscheidungsgrenze hat eine kreisförmige Struktur. Der Kernel-Trick nutz hier eine implizite Daten abbildung in einen höherdimensionalen Raum, in dem die Klassen leichter zu trennen sind.
Wir suchen hierfür einen Kernel \(K(\boldsymbol{x}_i, \boldsymbol{x}_j)\), der “ähnliche” Funktionswerte annimmt, wenn die Datenpunkte \(i\) und \(j\) zu derselben Klasse gehören. Für die in der Abbildung gezeigte Verteilung empfiehlt sich der polynomiale Kernel mit dem Grad \(d = 2\). Dieser Kernel berechnet die Ähnlichkeit zwischen zwei Datenpunkten \(\boldsymbol{x}_i\) und \(\boldsymbol{x}_j\) im Regressorraum als
\[\begin{align*} K(\boldsymbol{x}_i, \boldsymbol{x}_j) = \left( \sum_{l=1}^k x_{li} \cdot x_{lj} \right)^2. \end{align*}\]
Der polynomiale Kernel entspricht einer quadratischen Beziehung zwischen den Datenpunkten und ist so in der Lage, kreisförmige oder konzentrische Zusammenhänge im Regressorraum zu erfassen. Die Trennbarkeit der Beobachtungen aufgrund ähnlicher Werte des Kernels für Beobachtungen der selben Klasse kann hierbei durch eine explizite Transformation der Datenpunkte in einen höherdimensionalen Raum dargestellt werden. In unserem zwei-dimensionalen Beispiel ist diese Transformation
\[\begin{align} \begin{pmatrix} x = x_1\\ y = x_2 \end{pmatrix} \rightarrow \begin{pmatrix} x = x_1\\ y = x_2\\ z = x_1^2 + x_2^2. \end{pmatrix} \label{eq:polykerntrans} \end{align}\]
Die Abbildung \(\eqref{eq:polykerntrans}\) projiziert die Daten in den drei-dimensionalen Raum \(\mathbb{R}^3\), wobei die zusätzliche Koordinate \(z = x_1^2 + x_2^2\) die (quadratische) Distanz einer Beobachtung vom Ursprung darstellt. In diesem transformierten Raum sind konzentrisch angeordnete Klassen anhand des Wertes von \(z\) linear separierbar, was geometrisch einer trennenden Hyperebene entspricht. Durch die Wahl des polynomialen Kernels wird so eine nicht-lineare Trennlinie im ursprünglichen Regressor-Raum \(\mathbb{R}^2\) modelliert, welche die kreisförmige Entscheidungsgrenze erfassen kann.
Um dies grafisch zu veranschaulichen, transformieren wir die Datenpunkte in data_concentric gemäß der Funktion \(\eqref{eq:polykerntrans}\) nach \(\mathbb{R}^3\).
# Funktion: Explizite Transformation durch
# polynomiellen Kernel mit d = 2
poly_transform <- function(X) {
X1 <- X[, 1]
X2 <- X[, 2]
X_trans <- tibble(X1, X2, z = X1^2 + X2^2)
return(X_trans)
}
# Transformation furchführen
X_transformed <- poly_transform(
data_concentric %>%
dplyr::select(X1, X2)
)
# Transformierte Beobachtungen
slice_head(X_transformed, n = 5)# A tibble: 5 × 3
X1 X2 z
<dbl> <dbl> <dbl>
1 0.0380 0.535 0.288
2 0.863 -0.208 0.788
3 -0.514 -0.380 0.409
4 -0.936 -0.0886 0.883
5 -0.794 0.557 0.940Im nächsten Schritt berechnen wir für die transformierten Daten X_transformed unter Verwendung der Klassen in data_concentric$klasse einen SVC, also eine SVM mit linearem Kernel: Wir suchen eine trennende Ebene für die transformierten Daten X_transformed in \(\mathbb{R}^3\).
# SVM mit einem linearen Kernel
# auf den transformierten Daten trainieren
svm_model_poly_trans <- svm(
x = X_transformed,
y = data_concentric$klasse,
kernel = "linear"
)
svm_model_poly_trans
Call:
svm.default(x = X_transformed, y = data_concentric$klasse, kernel = "linear")
Parameters:
SVM-Type: C-classification
SVM-Kernel: linear
cost: 1
Number of Support Vectors: 27Die interaktive Abbildung 14.8 zeigt
- die transformierten Datenpunkte in \(\mathbb{R}^3\),
- die mit dem Modell-Objekt
svm_model_poly_transberechnete trennende Hyperebene (grün) und - die Support-Vektore der Hyperebene (grau hinterlegt).
Warning: 'rgl.viewpoint' is deprecated.
Use 'view3d' instead.
See help("Deprecated")data_concentric: In R3 linear separierbaren Datenpunkte und trennende Hyperebene
Beachte, dass die grüne Hyperebene die Daten nahezu perfekt trennt:
# Anteil falscher Klassifzikationen für data_concentric
1 - mean(predict(svm_model_poly_trans) == data_concentric$klasse)[1] 0.0025# SVM mit poly Kernel auf data_concentric trainiert
svm_model_poly <- svm(
x = data_concentric %>% dplyr::select(X1, X2),
y = data_concentric$klasse,
kernel = "polynomial",
coef0 = 0, # c = 0
degree = 2, # d = 2
gamma = 1,
cost = 1
)
svm_model_poly
Call:
svm.default(x = data_concentric %>% dplyr::select(X1, X2), y = data_concentric$klasse,
kernel = "polynomial", degree = 2, gamma = 1, coef0 = 0, cost = 1)
Parameters:
SVM-Type: C-classification
SVM-Kernel: polynomial
cost: 1
degree: 2
coef.0: 0
Number of Support Vectors: 24Die SVM-Modelle svm_model_poly_trans und svm_model_poly liefern identische Klassifzierungen der Beobachtungen in data_concentric.
Ahand der Komponenten des Objekts svm_model_poly und mit Vorhersagen der Klassen für ein Gitter von Punkten können wir die angepasste kreisförmige Entscheidungsgrenze sowie die Margins im urspünglichen Prädiktorraum \(\mathbb{R}^2\) visualisieren. Abbildung 14.9 zeig das Ergebnis.
grid <- expand_grid(
x1 = seq(min(data_concentric$X1), max(data_concentric$X1), length.out = 150),
x2 = seq(min(data_concentric$X2), max(data_concentric$X2), length.out = 150)
)
dist <- attributes(
predict(svm_model_poly, grid, decision.values = T)
)$decision.values
grid <- grid %>%
# Vorhersagen auf dem Grid
mutate(
distanz = dist,
klasse = predict(svm_model_poly, grid)
)
# Support-Vektoren
SV <- data_concentric %>%
slice(svm_model_poly$index)
ggplot(
data = data_concentric,
mapping = aes(x = X1, y = X2, color = klasse)
) +
geom_point(grid, mapping = aes(x = x1, y = x2, color = klasse), alpha = .01) +
geom_point() +
geom_contour(
data = grid,
aes(x = x1, y = x2, z = dist),
breaks = 0, # Decision boundary
color = "black",
) +
geom_contour(
data = grid,
aes(x = x1, y = x2, z = dist),
breaks = c(-1, 1), # Marginal lines
linetype = "dashed",
size = 0.5
) +
geom_point(
data = SV, inherit.aes = F,
mapping = aes(x = X1, y = X2),
shape = 1, size = 3
) +
coord_equal(expand = 0) +
theme_cowplot() +
theme(legend.position = "top")Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.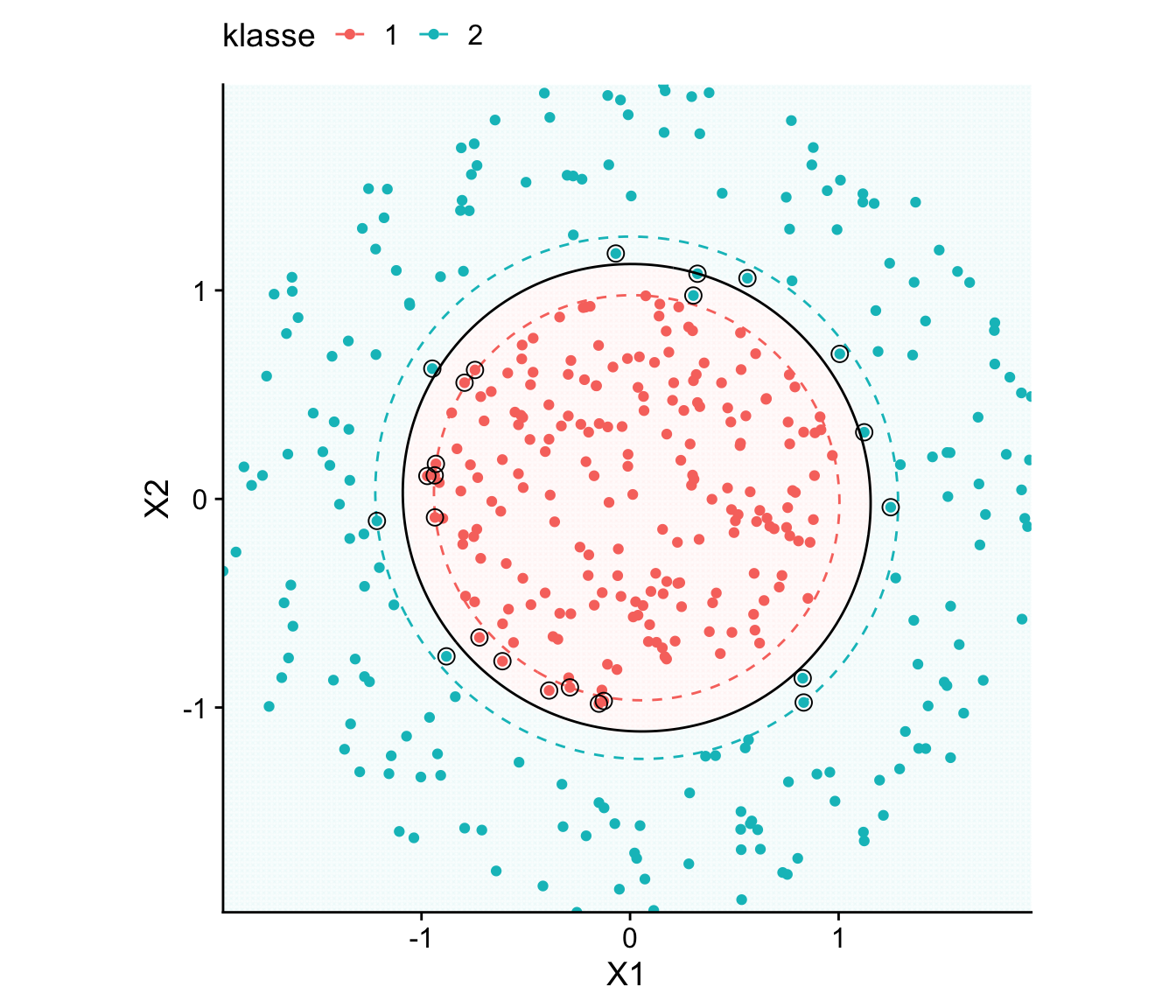
Dank des Kernel-Tricks können SVMs praktisch beliebige Formen von nicht-linearen Entscheidungsregeln lernen. Für die sinuidal verlaufende Entscheidungsgrenze im Datensatz data_wavy (vgl. Abbildung 14.5) ist ein radialer Kernel hilfreich:
Der radiale Kernel ist dem polynomiellen Kernel bei der Anpassung hochflexibler Entscheidungsgrenzen überlegen, weil er selbst stark variierende Muster dank großer lokale Flexibilität besser erfassen kann. Ein polynomialer Kernel hingegen ist durch seine funktionale Form und den Polynomgrad \(d\) beschränkt. Bei komplexen Grenzen muss \(d\) für mehr Flexibilität der SVM groß gewählt werden, was Overfitting begünstigen kann.
Für einen Vergleich mit der in Abbildung 14.5 visualisierten Anpassung des SVC trainieren nun eine SVM für data_wavy mit radialem Kernel als radial_svm_model für die Standardwerte cost = 1, coef0 = 0 und gamma = 1.
# SVM mit RBF-Kernel anpassen
radial_svm_model <- svm(
klasse ~ x2 + x1,
data = data_wavy,
kernel = "radial",
cost = 1,
coef0 = 0,
gamma = 1
)Wie zuvor plotten wir die trainierte Entscheidungsgrenze sowie die Margin gemeinsam mit mit den Datenpunkte im Regressor-Raum.
# Erzeuge einen Grid für die Vorhersagen
grid <- expand_grid(
x1 = seq(
min(data_wavy$x1),
max(data_wavy$x1),
length.out = 150),
x2 = seq(
min(data_wavy$x2),
max(data_wavy$x2),
length.out = 150
)
)
dist <- attributes(predict(radial_svm_model , grid, decision.values = T))$decision.values
grid <- grid %>%
# Vorhersagen auf dem Grid
mutate(
dist = dist,
klasse = predict(radial_svm_model , grid)
)
SV <- data_wavy %>%
slice(radial_svm_model$index)# Visualisiere die Entscheidungsgrenze mit ggplot2
ggplot() +
geom_point(
data = grid,
mapping = aes(x = x1, y = x2, color = klasse), alpha = 0.05) +
geom_point(
data = data_wavy,
mapping = aes(x = x1, y = x2, color = klasse)) +
geom_contour(
data = grid,
aes(x = x1, y = x2, z = dist),
breaks = 0, # Decision boundary
color = "black",
) +
geom_contour(
data = grid,
aes(x = x1, y = x2, z = dist),
breaks = c(-1, 1), # Marginal lines
linetype = "dashed",
size = 0.5,
color = "black"
) +
geom_point(
data = SV, inherit.aes = F,
mapping = aes(x = x1, y = x2),
shape = 1,
size = 3
) +
coord_equal() +
scale_x_continuous("X1", expand = c(0, 0)) +
scale_y_continuous("X2", expand = c(0, 0)) +
theme_cowplot() +
theme(legend.position = "top")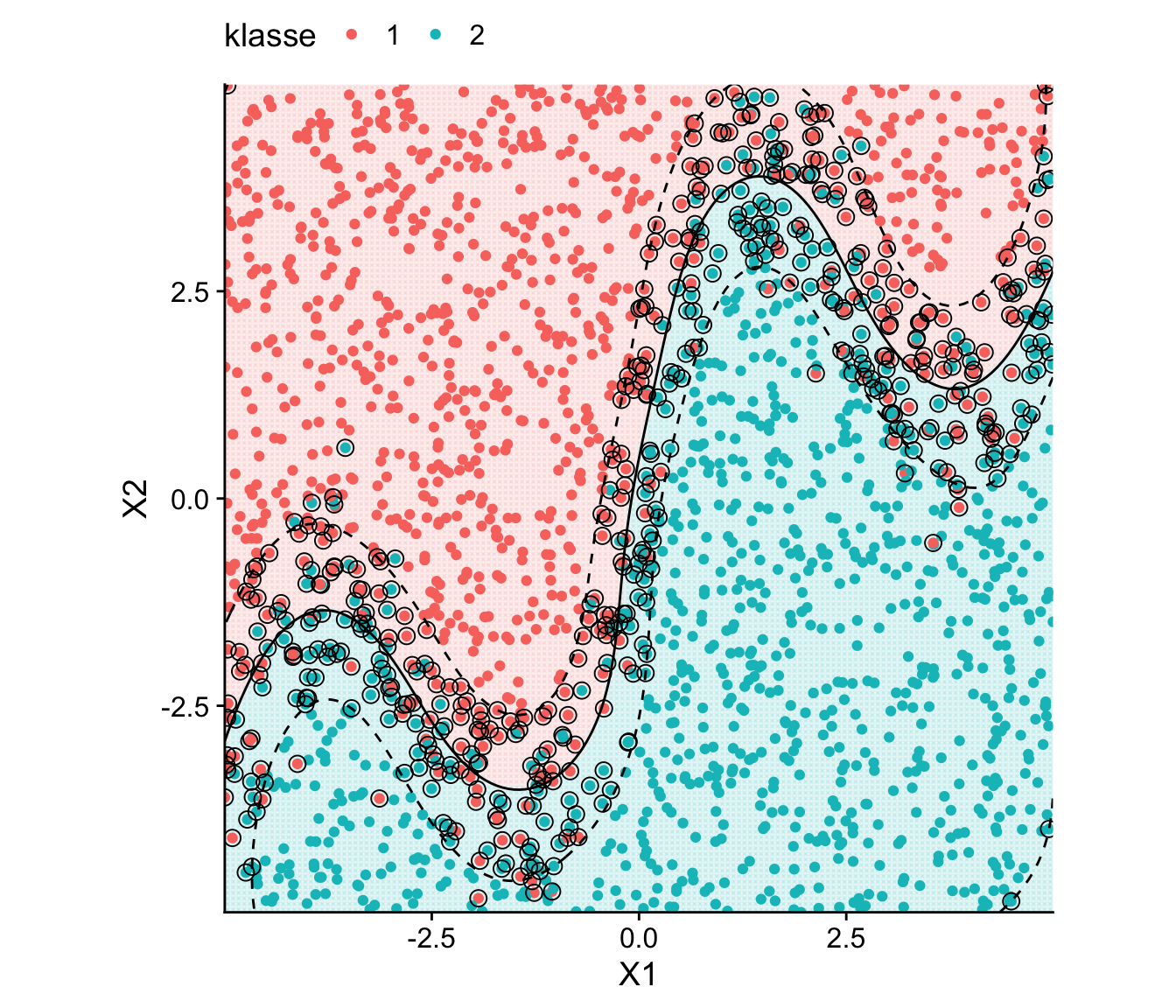
data_wavy mit RBF-SVM trainierte Entscheidungsgrenze
Ein Vergleich von Abbildung 14.10 mit Abbildung 14.6 zeigt, dass die SVM mit radialem Kernel im Objekt radial_svm_model den nicht-linearen Verlauf der sinusoidalen Entscheidungsgrenze deutlich besser erfasst als der SVC in svc_wavy. Der Anteil fehlklassifizierter Beobachtungen liegt bei weniger als 10%.
14.3.2 Overfitting
Der in Abschnitt Kapitel 14.2 beschriebene Einfluss des cost-Parameters auf die Klassifikationsleistung von SVCs überträgt sich auch auf SVMs. Bei der Anpassung nichtlinearer Entscheidungsgrenzen mit nichtlinearen Kernel-Funktionen müssen neben cost auch die Kernel-Parameter sorgfältig gewählt werden, um Overfitting zu vermeiden. Dabei bestehen Interdependenzen zwischen den Parametern. In den hier behandelten Beispielen mit einem zweidimensionalen Merkmalsraum lassen sich diese Effekte gut grafisch darstellen: Bei einer SVM mit radialem Kernel bewirken höhere gamma-Werte eine stärker lokal geprägte Entscheidungsgrenze, die sich enger um benachbarte Datenpunkte legt. Höhere cost-Werte führen zu engeren Margins, wodurch weniger Support-Vektoren zugelassen werden. Dies kann die Varianz der Entscheidungsgrenze erhöhen, da der Algorithmus sich stärker an einzelne Datenpunkte anpasst und die Schätzung tendenziell weiter von der wahren Grenze abweichen kann. Zu große Werte führen also jeweils zu einer Überanpassung an die Daten.
Wir illustrieren Overfitting durch eine ungünstige Parameterwahl für eine SVM mit Radial-Kernel und den Datensatz data_wavy.
# SVM mit ungünstiger Parameter-Kombination
radial_svm_overfit <- svm(
klasse ~ x2 + x1,
data = data_wavy,
kernel = "radial",
cost = 1000,
gamma = 10
)grid <- expand_grid(
x1 = seq(min(data_wavy$x1), max(data_wavy$x1), length.out = 150),
x2 = seq(min(data_wavy$x2), max(data_wavy$x2), length.out = 150)
)
dist <- attributes(predict(radial_svm_overfit , grid, decision.values = T))$decision.values
grid_overfit <- grid %>%
# Vorhersagen auf dem Grid
mutate(
dist = dist,
klasse = predict(radial_svm_overfit , grid)
)# Visualisiere die Entscheidungsgrenze mit ggplot2
ggplot() +
geom_point(
data = grid_overfit,
mapping = aes(x = x1, y = x2, color = klasse), alpha = 0.1) +
geom_point(
data = data_wavy,
mapping = aes(x = x1, y = x2, color = klasse)) +
geom_contour(
data = grid_overfit,
aes(x = x1, y = x2, z = dist),
breaks = 0, # Decision boundary
color = "black",
) +
geom_contour(
data = grid_overfit,
aes(x = x1, y = x2, z = dist),
breaks = c(-1, 1), # Marginal lines
linetype = "dashed",
size = 0.5,
color = "black"
) +
coord_equal() +
scale_x_continuous("X1", expand = c(0, 0)) +
scale_y_continuous("X2", expand = c(0, 0)) +
theme_cowplot() +
theme(legend.position = "top")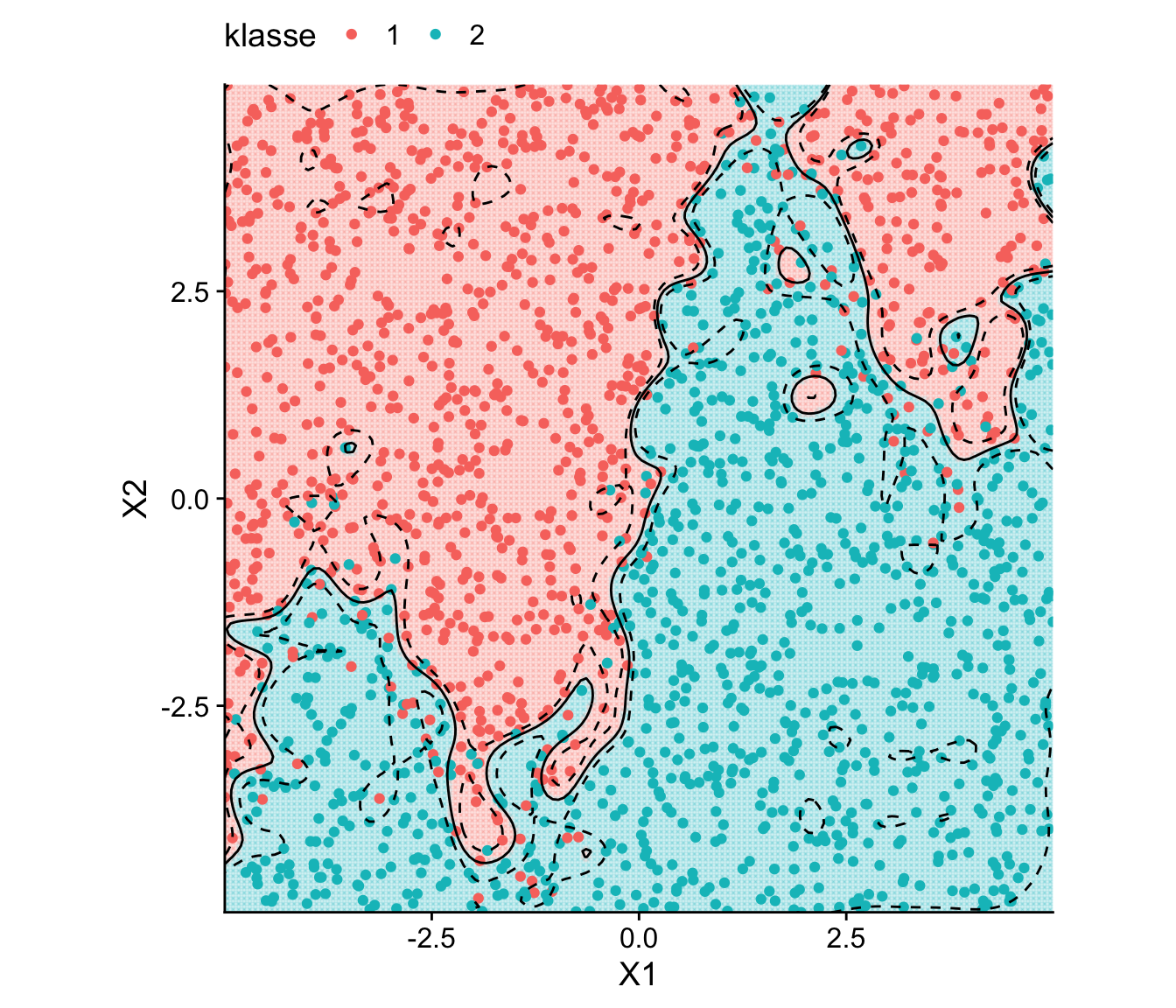
data_wavy: Overfitting der Entscheidungsgrenze mit RBF-SVM
# Fehlklassifikationsrate bei Overfitting:
1 - mean(
predict(radial_svm_overfit) == data_wavy$klasse
)[1] 0.058Das Modell radial_svm_overfit leidet unter Overfiting: In Abbildung 14.11 sehen wir, dass die gelernte Entscheidungsgrenze zu stark durch lokale Muster aufgrund der Überlappung der Klassen geprägt ist. Entsprechend ist die Klassifikation der für das Training genutzen Datenpunkte für radial_svm_overfit etwas genauer radial_svm_model. Diese Überanpassung resultiert tendentiell in einer schlechteren Generalisierung von radial_svm_overfit in Vorhersagen unbekannter Datenpunkte.
Mit e1071::tune() können wir optimale Parameterwerte aus einem Grid mit Cross-Validation schätzen. Wir übergeben hierzu die Methode (METHOD), die Spezifikation des Modells wie in svm() und dem Argument ranges die zu berücksichtigenden Parameter-Werte als Liste.
set.seed(1234)
# Cross-Validation für Parameter in radialer SVM
radial_svm_tuned <- tune(
METHOD = svm,
klasse ~ x2 + x1,
data = data_wavy,
kernel = "radial",
# Parameter-Werte festlegen
ranges = list(
cost = c(1, 2, 4, 6),
gamma = c(0, .01, .05, .1, .25, .5, .8, 1, 2, 3)
)
)
# CV-Ergebnisse auslesen
radial_svm_tuned$performances cost gamma error dispersion
1 1 0.00 0.4960 0.02282786
2 2 0.00 0.4960 0.02282786
3 4 0.00 0.4960 0.02282786
4 6 0.00 0.4960 0.02282786
5 1 0.01 0.1835 0.03308659
6 2 0.01 0.1835 0.03240799
7 4 0.01 0.1830 0.03110913
8 6 0.01 0.1830 0.03038640
9 1 0.05 0.1745 0.03148633
10 2 0.05 0.1720 0.02679138
11 4 0.05 0.1665 0.02273641
12 6 0.05 0.1630 0.02335713
13 1 0.10 0.1595 0.02254009
14 2 0.10 0.1495 0.02033743
15 4 0.10 0.1450 0.01914854
16 6 0.10 0.1420 0.01584649
17 1 0.25 0.1360 0.01429841
18 2 0.25 0.1295 0.01657475
19 4 0.25 0.1230 0.01475730
20 6 0.25 0.1190 0.01370320
21 1 0.50 0.1150 0.01452966
22 2 0.50 0.1080 0.02188353
23 4 0.50 0.1000 0.02108185
24 6 0.50 0.0910 0.01696401
25 1 0.80 0.1005 0.01992346
26 2 0.80 0.0915 0.02041922
27 4 0.80 0.0885 0.01901023
28 6 0.80 0.0875 0.01703754
29 1 1.00 0.0950 0.01840894
30 2 1.00 0.0900 0.02041241
31 4 1.00 0.0865 0.01650757
32 6 1.00 0.0850 0.01763834
33 1 2.00 0.0890 0.01940790
34 2 2.00 0.0860 0.01897367
35 4 2.00 0.0905 0.01992346
36 6 2.00 0.0905 0.01921371
37 1 3.00 0.0900 0.02000000
38 2 3.00 0.0915 0.01716748
39 4 3.00 0.0925 0.01859659
40 6 3.00 0.0920 0.01798147error ist die mithilfe von Cross-Validation geschätzte Fehlklassifikationsrate für unbekannte Beobachtungen. Die Ergebnisse verdeutlichen, dass die Modellleistung stark von der Fähigkeit des radialen Kernels abhängt, Nicht-Linearitäten zu erfassen: Bereits geringe gamma-Werte führen zu einer signifikanten Reduktion der Fehlklassifikationsrate im Vergleich zu einem trivialen Modell mit gamma = 0.7
7 Für gamma = 0 wird lediglich eine Konstante angepasst, es findet also extremes “Underfitting” statt: Das Modell ist dann nicht besser als die zufällige Klassifikation mit Wahrscheinlichkeiten, die den relativen Häufigkeiten der Klassen im Datensatz entsprechen (baseline accuracy).
# Beste Parameter-Kombination anzeigen
radial_svm_tuned$best.parameters cost gamma
32 6 1# Beste SVM auslesen
radial_svm_tuned$best.model
Call:
best.tune(METHOD = svm, train.x = klasse ~ x2 + x1, data = data_wavy,
ranges = list(cost = c(1, 2, 4, 6), gamma = c(0, 0.01, 0.05,
0.1, 0.25, 0.5, 0.8, 1, 2, 3)), kernel = "radial")
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 6
Number of Support Vectors: 45014.4 Beispiel: Vorhersage von Kaufentscheidungen
Der mit dem R-Paket ISLR (James u. a. 2021) Datensatz OJ enthält Beobachtungen von 1070 Orangensaft-Verkäufen bei denen der Kunde entweder die Marke “Citrus Hill” (CH) oder “Minute Maid” (MM) gekauft hat. Tabelle 14.1 enthält eine Beschreibung der verfügbaren Variablen.
| Variable | Beschreibung |
|---|---|
| Purchase | Kauf von CH oder MM Orangensaft |
| WeekofPurchase | Kaufwoche |
| StoreID | ID des Geschäfts |
| PriceCH | Preis für Citrus Hill |
| PriceMM | Preis für Minute Maid |
| DiscCH | Rabatt auf Citrus Hill |
| DiscMM | Rabatt auf Minute Maid |
| SpecialCH | Sonderangebot für Citrus Hill |
| SpecialMM | Sonderangebot für Minute Maid |
| LoyalCH | Markentreue für Citrus Hill |
| SalePriceMM | Verkaufspreis für Minute Maid |
| SalePriceCH | Verkaufspreis für Citrus Hill |
| PriceDiff | Unterschied Verkaufspreise MM - CH |
| Store7 | Verkauf in Geschäft 7 (Ja/Nein) |
| PctDiscMM | Prozentualer Rabatt für MM |
| PctDiscCH | Prozentualer Rabatt für CH |
| ListPriceDiff | Unterschied Listenpreise MM - CH |
| STORE | Welches der 5 möglichen Geschäfte |
OJ: Übersicht der Variablen
Nach Laden des Pakets fügen wir den Datensatz OJ der Arbeitsumgebung hinzu. Wir transformieren WeekofPurchase in eine leichter intepretierbare Wochenangabe und definieren die kategorischen Variablen als Typ factor.
Der nächste Code-Chunk produziert eine Grafik für die Gesamtenwicklung der Verkäufe über das Jahr.
Mit ggcorrplot::ggcorrplot() erzeugen wir einen Korrelationsplot für die numerischen Variablen des Datensatzes, um die linearen Zusammenhänge zwischen den Preis-, Rabatt- und Verkaufsvariablen einzuschätzen.
Die Abbildung zeigt, dass es starke Korrelation zwischen Discount-Indikatoren (DiscCH, DiscMM) und den jeweiligen Prozent-Beträgen (PctDiscCH, PctDiscMM) sowie der Preis-Differenz (PriceDiff) gibt. Die Variablen STORE und Store7 enthalten redundante Informationen über das Geschäft, in dem der Verkauf stattfand. Wir entfernen diese Variablen bevor der Datensatz mit rsample::initial_split() in Trainings- und Test-Partitionen eingeteilt wird.
Mit recipe::recipe() können Datensätze systematisch für die Anwendung von Machine-Learning-Methoden vorbereitet werden. Im nachfolgenden Code-Chunk erstellen wir das recipe blueprint: Wir skalieren und zentrieren wir numerische Variablen, was sicherstellt, dass die Regresoren auf einer vergleichbaren Skala liegen, sodass distanzbasierte Algorithmen nicht durch unterschiedliche Skalierungen Variablen beeinflusst werden. Kategorische Variablen mit mehr als zwei Ausprägungen werden mithilfe von One-Hot-Encoding in binäre Dummy-Variablen umgewandelt. Dieser Ansatz sorgt für eine konsistente und reproduzierbare Datenvorverarbeitung jenseits der Anwendungen mit SVMs.
Mit recipes::prep() bestimmen wir die nötigen Parameter für die Vorbereitung von Datensätzen mit dem in oj_train enthaltenen. recipes::bake() wendet die Transformationen an. Wir erzeugen eine Übersicht der transformierten Trainingsdaten mit skimr::skim.
Die nächsten Code chunks zeigen, wie parsnip SVMs mit lineare, polynomialen und radialen Kernel-Funktionen für die Klassifikation der gekauften Orangensaft-Marke Purchase angepasst werden können. Dabei wird die Implentierung von ksvm() im Paket kernlab genutzt. Für jeden dieser drei Ansätze definieren wir einen separaten Workflow für 10-fache Cross-Validation der jeweiligen Modellparameter.8 Als Kriterium für die Modellleistung verwenden wir accuracy, den Anteil korrekter Klassifikationen. Nach Anpassung des als optimal ermittelten Modells evaluieren wir die Vorhersagegenauigkeit der Modelle auf dem Testdatensatz bake_train.
8 Aufgrund der geringen Rechenleistung der für die interaktiven Code-Chunks genutzen Webr-Implementierung betrachten wir hier beispielhafte, kleine Parameter-Gitter.
SVM: Linearer Kernel
SVM: Radialer Kernel
SVM: Polynomialer Kernel
Für einen tabellarischen Vergleich der Performance der Modelle auf den Testdatensatz sammeln wir die Ergebnisse in einer Liste ergebnisse und verwenden purrr::map_dfr() für die Transformation in eine tibble mit der ID-Variable Modell. Die Metrik accuracy tabellieren wir mit gt::gt().
Die Auswertung zeigt, dass die hier betrachteten SVMs mit nicht-linearer Kernelfunktion den SVC mit linearem Kernel hinsichtlich der Genauigkeit der Vorhersagen auf dem Testdatensatz nicht schlagen können.
14.5 Zusammenfassung
In diesem Kapitel haben wir Support Vector Machines (SVM) zur Klassifikation eingeführt, eine Machine-Learning-Methode, die sich besonders für komplexe und nicht-lineare Probleme in hochdimensionalen Datensätzen eignet. Das Ziel von SVMs ist es, eine Trennlinie oder -ebene im Regressorraum zu finden, die zwei Klassen von Datenpunkten optimal voneinander abgrenzt. Hierfür ermittelt ein Algorithmus sogenannte Support-Vektoren – eine Teilmenge der Datenpunkte, welche die angepasste Entscheidungsgrenze bestimmen.
Support Vector Machines (SVMs) sind eine Weiterentwicklung des klassischen Maximal Margin Classifiers (MMC). Während der MMC eine harte Trennlinie sucht, die die Daten perfekt in zwei Klassen unterteilt, funktioniert dieser Ansatz nur dann gut, wenn die Klassen klar separierbar sind. Bei realen Datensätzen, in denen Überlappungen oder Ausreißer auftreten, scheitert der MMC-Algorithmus. Hier kann ein Soft Margin Classifier (SMC) angewendet werden, eine Verallgemeinerung des MMC, die Fehlklassifikationen zulässt. Diese zusätzliche Flexibilität erweitert die Anwendbarkeit auf reale, häufig nicht perfekt linear trennbare Klassen.
Für Klassifikationsprobleme mit nicht-linearen Entscheidungsgrenzen wird das Prinzip des SMCs durch den sogenannten Kernel-Trick zu einer SVM erweitert. Hierbei werden die Daten implizit in einen höherdimensionalen Raum projiziert, ohne dass die Transformation explizit durchgeführt werden muss. In diesem Raum lassen sich ursprünglich komplexe Entscheidungsgrenzen durch eine (lineare) Hyperebene modellieren. Unterschiedliche Kernel-Funktionen wie der radiale Kernel oder der polynomiale Kernel erlauben es, verschiedene Formen nicht-linearer Entscheidungsgrenzen zu erfassen und anzupassen.
Die Implementierung von SVMs in R erfolgt effizient durch Pakete wie e1071 und kernlab. Wir haben gezeigt, wie Datensätze mithilfe von parsnip im tidymodels-Framework systematisch vorbereitet, SVM-Modelle spezifiziert, durch Cross-Validation optimiert und vergleichen werden können.